AI 也有蝴蝶效應，人工智慧用到的數學理論？最陡下降法、區域解、模糊理論、混沌——《從人到人工智慧，破解 AI 革命的 68 個核心概念》

2017 年 06 月 27 日

技術Ｘ解析

編按：AI 的運作與演進一直和數學息息相關，在《從人到人工智慧，破解 AI 革命的 68 個核心概念：實戰專家全圖解 × 人腦不被電腦淘汰的關鍵思考》中，作者告訴我們高科技的 AI 到底是使用哪種數學？本文選自第 13 章〈人工智慧使用的數學〉，一起來弄懂「最陡下降法、區域解、模糊理論、混沌」是什麼。

文／三宅陽一郎、森川幸人

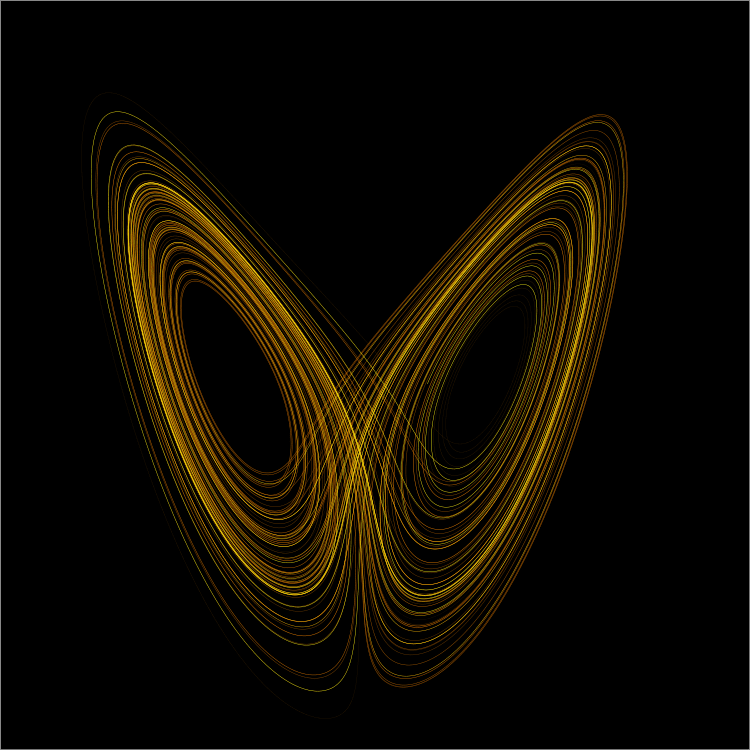
氣象學家羅倫茲（Edward Lorenz）在 1960 年代發現「蝴蝶效應」。上為羅倫茲吸子圖形。（By User:Wikimol, User:Dschwen GFDL, via Wikimedia Commons）

最陡下降法（steepest descent method）

最陡下降法是利用類神經網路的誤差倒傳遞，運用於學習的收斂演算法。要用有限步驟解給定函數的近似解，就會用這種方法。

用最簡單的單一變數的函數來說明，從函數上任意一點開始，從那裡拉出切線。該切線與 X 軸的交點的 X 座標，視為函數上的一點。接著再從這裡，和前面一樣，「拉出切線」，反覆進行這樣的步驟，就會越來越接近該函數的解。

依據初始值的不同，有時會出現無法收斂解的狀況。此外，不保證一定可以收斂。感知器型類神經網路的誤差倒傳遞之所以可以收斂，是因為這個最陡下降法用比一般更多的變數而成立的緣故。

以另一個角度來觀察，使用最陡下降法時，初始值設定為多少，會決定最後收斂的解。若以複變函數（complex function）來進行，複數平面（complex plane）上的任意點，決定了該複變函數收斂於哪個解。將收斂於哪個解用顏色區分，就會出現碎形圖（fractal graphic）。例如，Z3=1 這樣簡單的函數，也會出現碎形。可以說，最陡下降法具有混沌的初始值敏銳性。

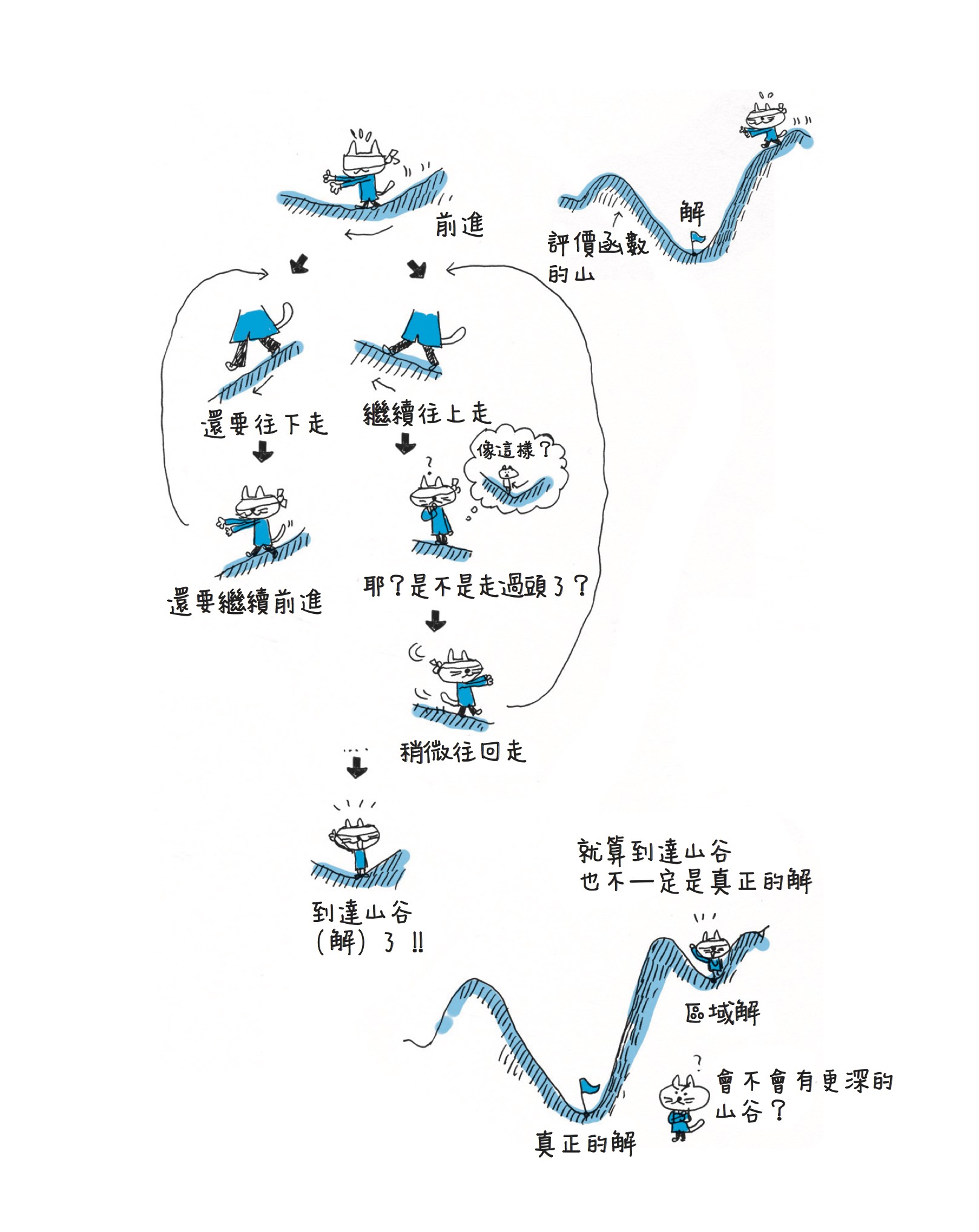
區域解（local solution）

區域解原是數學的概念，表示在方程式的解當中，收斂於某一個解。區域最小值（local minimum）則是指只在該解的區域附近，取得最小值的點，但它不是全域最小值（global minimum）。

在軟體上解方程式，必須用有限的步驟趨近解，但在達到區域最小值時會停止。這種現象稱為「陷入區域最小值」。這表示尚未找到真正的解，而是找到區域解就停止了，是無效的。日常生活中也會用比喻的方式說「你的想法陷入區域最小值了」，藉以批評「只用狹隘的觀點思考」。

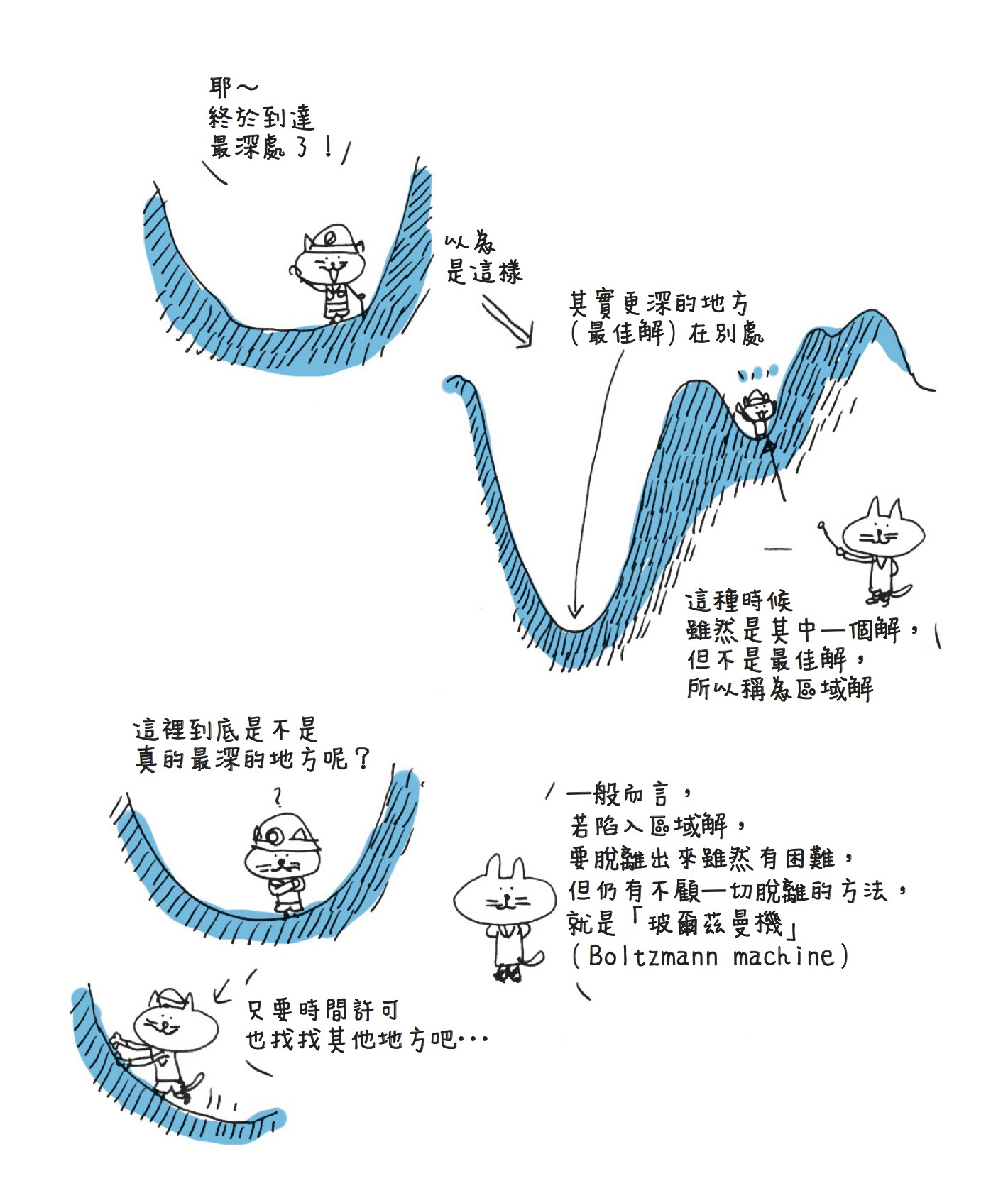
^譯注：玻爾茲曼機是隨機神經網絡和遞歸神經網絡的一種，最早能夠學習內部表達，並能表達和（給定充足的時間）解決複雜的組合優化問題的神經網絡。

模糊理論（fuzzy theory）

我們平常談到高度、熱度、數量、重量等「度量」，不一定會講出精密的度量值，而是說個概略的數字。以數理方式來處理這種模糊的度量，方法之一是區分為某數值以上、某數值以下來思考。然而，模糊理論要求「使用數理表現方式時保留模糊狀態」。

以模糊理論來討論身高，設定超過某值就是身高高的數值，以及低於某值就是身高矮的數值。舉例來說，超過 180 公分就是身高高、不到 150 公分就是身高矮。此時，身高 180 公分（以上）的人表示為「身高高度值1」，身高 150 公分（以下）的人表示為「身高高度值0」。於是，身高 170 公分的人「身高高度值 0.7」，身高 160 公分的人「身高高度值 0.3」。

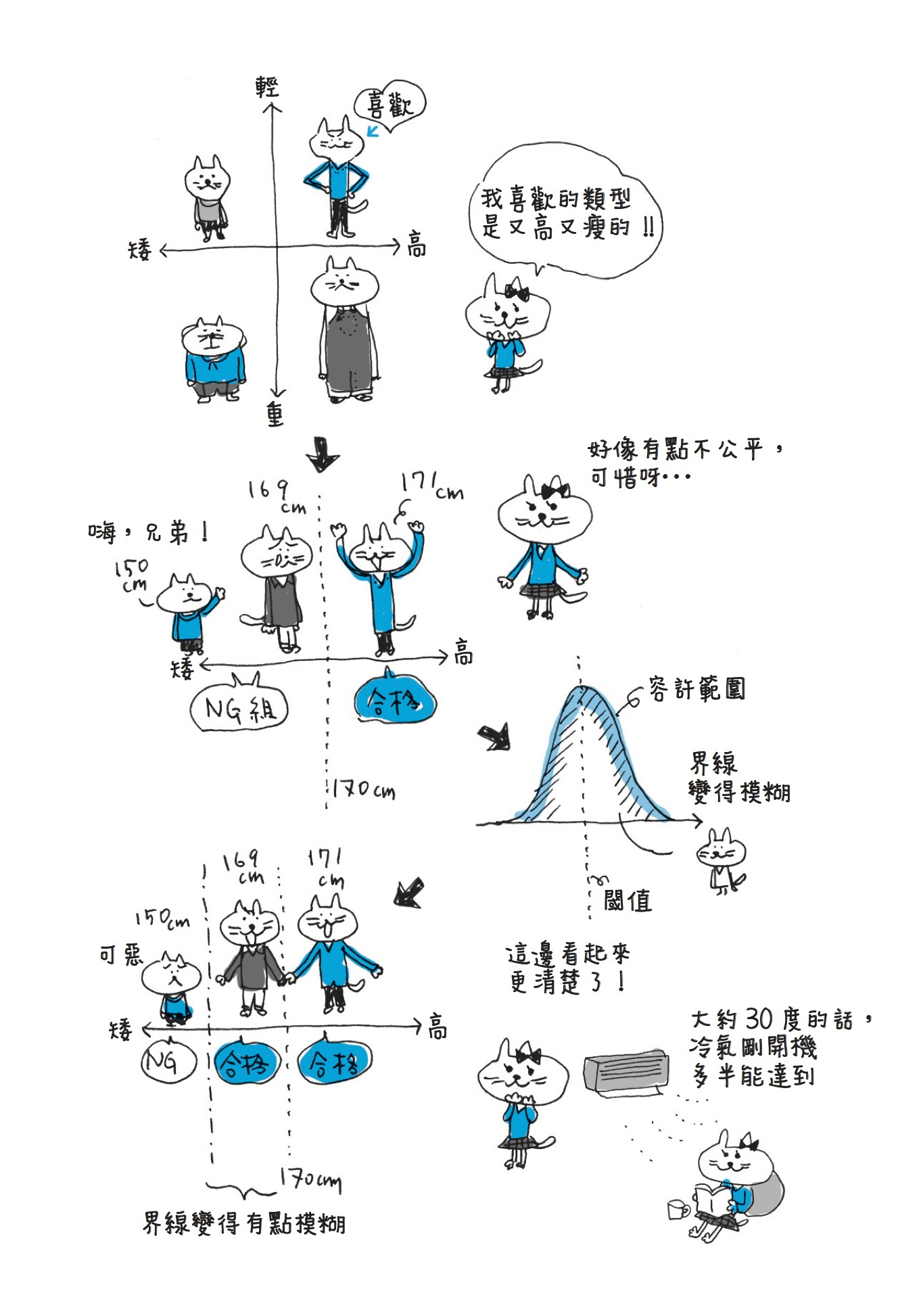
像這樣，把所有的身高都用「身高高度值 0 至 1」來表示。這樣一來，身高 180 公分的人和身高 179 公分的人就不會只差 1 公分，卻被分成高和矮，得以避免這種不合邏輯的劃分。

現在空調機配備了所謂「fuzzy 功能」，這是指可以對應「有點熱」或「非常冷」這種模糊的感覺的意思。

混沌（chaos）

有一段時間，混沌、碎形、1／ƒ 噪音（粉紅雜訊 pink noise）、fuzzy（模糊）等詞彙，可見於家電製品等的行銷。

^譯注：1／ƒ 噪音是自然界最常見的噪音，從功率的角度來看，這種噪音的能量從低頻向高頻不斷衰減，曲線為1／ƒ。

chaos（混沌）一詞的字源是古希臘文 khaos。一般而言，混沌的定義如下：

某系統在某時間點的狀態（＝初始值）決定好之後，原則上其後的狀態都已決定，不遵循這樣的決定論法則，產生非常複雜且不規則、不穩定的行為，不可能預測遙遠未來狀態的現象。

簡言之，就是「雖然理論上可以計算，實際上未來數值會如何無法準確預估的現象」。

1961 年，氣象學家羅倫茲（Edward Lorenz）建構預測天氣的方程式，進行了兩次計算。然而，得到的答案完全不同。檢查後發現，第一次計算時給定的初始值到小數點後六位，第二次計算（驗證）給定的初始值到小數點後三位，查明了這就是原因。

當時還沒有混沌的觀念，認為就算小數點後六位的數據寫成小數點後三位，對計算結果應該影響不大。但是這微小的差異卻造成計算結果巨大的差別。

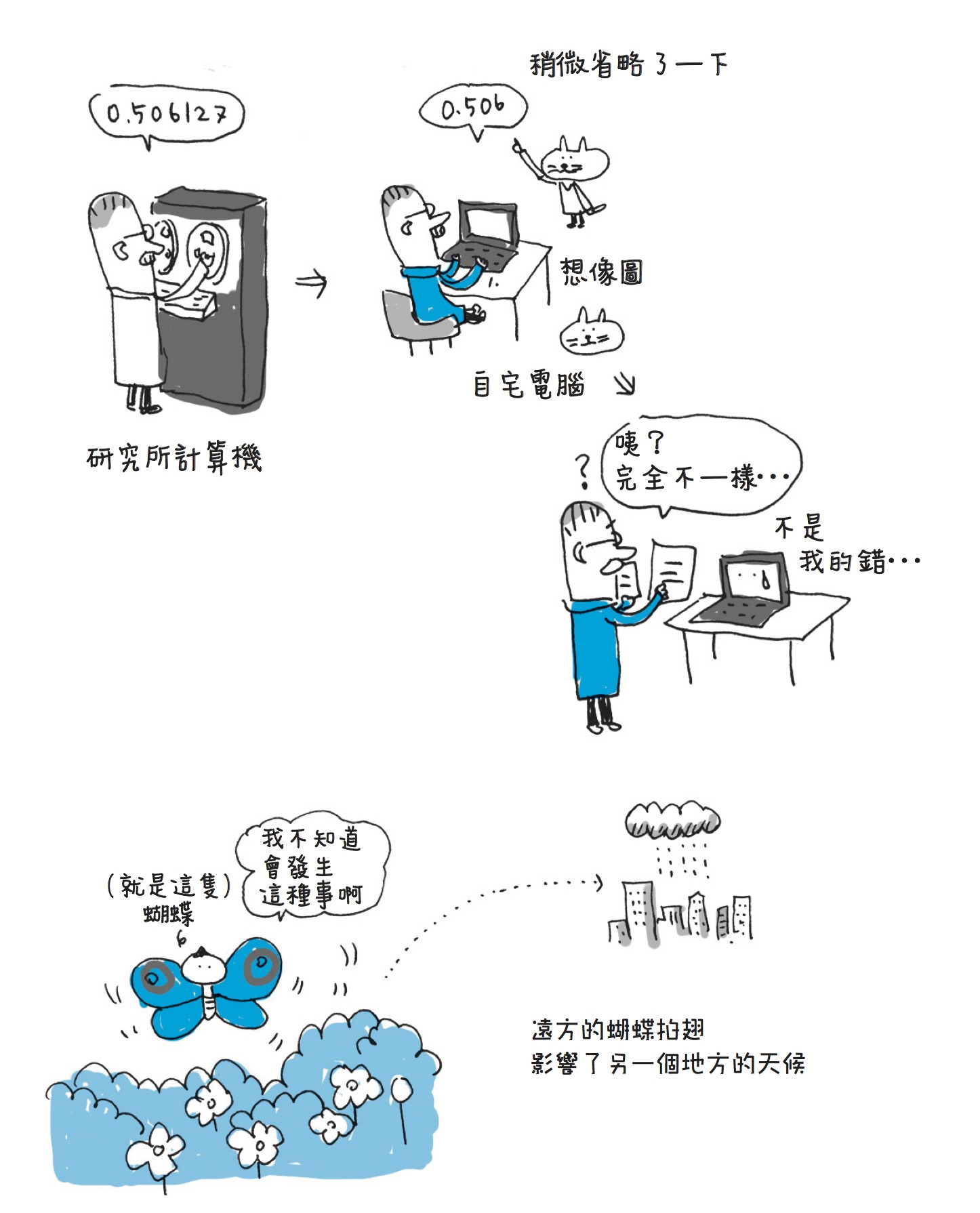
微小的差異造成巨大差別的現象，稱為蝴蝶效應（butterfly effect）。

一隻蝴蝶在巴西輕拍翅膀，使周圍的空氣波動，產生了熱氣。這是非常微小的量，但仍對大氣造成些微影響。這個影響的連鎖反應，很快也對氣象帶來影響，終於在數星期後，在遙遠的美國德州引起颶風。

這樣的混沌現象，不是只發生在物理學或數學的世界。我們身體的心跳數、腦波、呼吸，以及想要記住東西時神經元的興奮，都存在著混沌的行為（也就是稍微脫離規律）。有一種說法認為，生病時這種混沌的行為會消失，呼吸和其他功能變得非常規律。「正常狀況＝混沌波動的狀況」，才是我們生物原有的樣子。突如其來的想法，或是靈光乍現的創意，或許就是這種混沌波動所帶來的最終效果。

（本文摘自《從人到人工智慧，破解 AI 革命的 68 個核心概念》）